Quello che segue vuole mostrare quanto la natura possa essere complessa e lontana dal senso comune quando andiamo a considerare fenomeni che avvengono su scala estremamente piccola. Il pretesto è un problema all'apparenza molto semplice: misurare la carica elettrica di un elettrone.
Ovviamente dal punto di vista strettamente sperimentale la cosa può essere decisamente complicata, ma la premessa è che non ci preoccuperemo degli aspetti tecnico-pratici, che certamente hanno un ruolo importante se si vuole effettuare questa misura, ma analizzeremo la questione dal punto di vista strettamente concettuale.
Idealmente, per misurare la carica dell'elettrone, potremmo prendere due elettroni, metterli a una certa distanza nello spazio, e misurare la forza che li spinge ad allontanarsi fra loro. Questo è un semplice problema di elettrostatica, al quale applicheremo la legge di Coulomb: nota la distanza, e misurata la forza che agisce fra le due cariche, ricaveremo il valore della carica elettrica delle due particelle.
Uno potrebbe obiettare che è difficile tenere fermi due elettroni e misurarne la forza, anche senza scomodare il principio di indeterminazione, per cui, più concretamente, potremmo porre un certo numero di elettroni su un elettrodo di un condensatore, e misurare la tensione risultante. Il valore che ricaveremmo è quello che si trova sui libri per la carica dell'elettrone: q = 1.60217662 × 10-19C (C=Coulombs, l'unità di misura della carica elettrica). Questo numero, se elevato al quadrato e diviso per ħ (la costante di Planck diviso 2 pigreco) e la velocità della luce c, è una quantità adimensionale (è un numero puro, senza unità di misura) che vale circa 1/137. Si chiama costante di struttura fine, e è una delle costanti fondamentali della Natura.
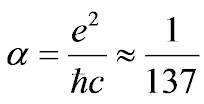 |
| La costante di Struttura Fine: e è la carica dell'elettrone, h tagliato è la costante di Planck divisa per 2 pigreco, c è la velocità della luce. Il suo valore è circa 1 su 137. |
Quella che abbiamo appena descritto è una misura di tipo statico: gli elettroni stanno fermi, o al massimo si agitano un po' sugli elettrodi del condensatore.
Però potremmo agire in un altro modo. Potremo prendere un elettrone, e spararlo contro un altro elettrone, oppure sparare due elettroni uno contro l'altro, che alla fine è poi la stessa cosa. Gli elettroni, avvicinandosi, si respingeranno a vicenda, modificando la loro traiettoria, e verranno deflessi. Il modo in cui verranno deflessi, che è calcolabile, dipende dalla loro carica elettrica e dal parametro di impatto, cioè in sostanza da quanto al massimo si possono avvicinare reciprocamente, avendo cercato di prendere bene la mira.
Questo modo di misurare la carica dell'elettrone, diverso dal precedente dal punto di vista del metodo, è di tipo dinamico: risaliamo cioè al valore della carica dell'elettrone in base a come i due elettroni si muovono mentre si respingono fra loro, misurando come le loro traiettorie vengono deflesse se li lanciamo uno contro l'altro.
Però i risultati dovrebbero essere identici. E infatti lo sono: l'urto ci mostra un comportamento che è il risultato della legge di Coulomb per due elettroni in movimento. I due elettroni si respingono mentre si avvicinano, interagendo fra loro secondo una legge che varia con l'inverso del quadrato della loro distanza. Le loro traiettorie sono il risultato di questo tipo di interazione, e dallo studio delle loro traiettorie possiamo ricavare il valore delle loro cariche elettriche. E il risultato, per il valore della carica dell'elettrone, è sempre lo stesso.
Adesso però cerchiamo di sparare i due elettroni uno contro l'altro cercando di prendere bene la mira, e dando loro un grande impulso, in modo che si avvicinino il più possibile, cercando di vincere la loro repulsione elettrica. E cerchiamo di farlo aumentando ogni volta sempre di più il loro impulso.
Se facciamo questo, succedono cose strane. Il modo in cui i due elettroni si comportano se prendiamo molto bene la mira, e conferiamo loro un grande impulso, è tale che la carica elettrica dell'elettrone, che ricaviamo dalle traiettorie degli elettroni durante l'urto, sembra aumentare al crescere dell'impulso che si scambiano i due elettroni. Il valore della costante di struttura fine che misuriamo, in pratica, cresce con il crescere dell'energia dell'urto con cui cerchiamo di misurarlo.
La domanda a questo punto è: come è possibile che una quantità che è il prodotto di costanti fondamentali della natura, non sia affatto costante? Cosa succede alla carica dell'elettrone? Come può essa variare a seconda dell'impulso scambiato dai due elettroni durante l'urto?
Ce lo spiega l'elettrodinamica quantistica e la teoria dei campi quantistici. Calmi, niente panico!
Per capire cosa succede, vediamo che cosa implichi aumentare l'impulso dei due elettroni che vanno a interagire reciprocamente. Aumentare l'impulso vuol dire diminuire di conseguenza la lunghezza d'onda di De Broglie dell'elettrone: maggiore è l'impulso di una particella, minore è la sua lunghezza d'onda associata. Questo permette in pratica agli elettroni di "scrutarsi" reciprocamente con maggiore risoluzione.
D'altra parte è così che funziona un microscopio elettronico: se vogliamo vedere qualcosa di molto piccolo, invece di usare un fascio di luce, la cui lunghezza d'onda è troppo grande per "vedere", ad esempio, la struttura di un cristallo, si usa un microscopio elettronico, nel quale al posto della luce, per illuminare l'oggetto che voglio studiare, uso un fascio di elettroni opportunamente accelerato.
Quando questo fascio di elettroni interagisce con l'oggetto da studiare, la sua lunghezza d'onda, determinata dosando l'impulso del fascio di elettroni in modo da essere sufficiente piccola, è capace di "vedere" i dettagli dell'oggetto che ci interessano. In pratica l'interazione dell'elettrone avviene con i dettagli dell'oggetto posti sul "vetrino", e questi dettagli sono tanto più piccoli tanto maggiore è l'impulso degli elettroni. Questo ci permette di vedere, tramite un microscopio elettronico, dettagli altrimenti invisibili con un normale microscopio ottico, che cioè sfrutta la luce per illuminare ciò che vogliamo vedere, e che quindi non potrà mai mostrarci dettagli più piccoli della lunghezza d'onda della luce visibile, non importa quanto siano buone le lenti.
Quindi, quando lanciamo un elettrone contro l'altro, ad esempio in un acceleratore di particelle, i due elettroni, grazie alla loro piccola lunghezza d'onda di De Broglie, che è tanto più piccola tanto maggiore è il loro impulso, si "scrutano" da molto vicino, e sono capaci di vedere cose che, ad elettroni che si avvicinano con un basso impulso reciproco, risulterebbero invisibili.
E sebbene - per quanto ne sappiamo - gli elettroni non abbiano una struttura interna (nel senso che gli esperimento fatti finora non hanno mai evidenziato che gli elettroni siano composti di sottostrutture) quando si scrutano così in dettaglio si accorgono che lo spazio attorno ad essi, a risoluzioni spaziali così estreme, è tutt'altro che vuoto, ma appare come polarizzato dalla loro presenza, ovvero dalle loro cariche elettriche, come se fosse un dielettrico. Questa polarizzazione si manifesta circondando i due elettroni di una moltitudine di coppie elettrone-positrone (il positrone è l'antiparticella dell'elettrone). Aumentando l'impulso degli elettroni, riusciamo però a penetrare dentro questa nube, che dall'esterno funge da parziale schermo alla "vera" carica dell'elettrone.
E il risultato è che la carica di un elettrone ci appare variare con l'impulso dell'elettrone sonda con cui lo studiamo. Se ad esempio misuriamo la carica dell'elettrone con elettroni dall'energia di 100 GeV o più, come accade nei moderni acceleratori, tipo il LEP del Cern, che ha raccolto dati nell'ultimo decennio del secolo scorso, la costante di struttura fine passa da 1/137 dei libri, a circa 1/128.
Ci tengo a sottolineare che il fenomeno della polarizzazione del vuoto, sebbene possa sembrare fantascientifico, è così ben descritto dall'elettrodinamica quantistica che le previsioni teoriche delle quantità osservabili combaciano con le misure sperimentali con precisioni altissime, tanto da rappresentare le misure più precise in assoluto in fisica. Nessun altra misura in fisica, di nessun tipo, può vantare un confronto teoria-esperimento così perfetto.
 |
| L'evoluzione dell'inverso della costante di struttura fine in funzione del quadri-impulso trasferito nell'urto. La linea continua è la previsione teorica secondo l'elettrodinamica quantistica (QED). |
Un effetto simile accade anche con la costante di accoppiamento delle interazioni nucleari forti. In questo caso, però, l'effetto è opposto. L'interazione fra due quark è infatti "forte" a distanze "grandi" (in questo caso "grandi" sono le distanze tipiche dei protoni dentro un nucleo), cosa che impedisce di riuscire a strappare un quark dall'interno di un protone, perché allontanandolo dagli altri quark la forza che li tiene assieme diventa enorme. Però, se aumentiamo l'energia a cui facciamo scontrare due protoni, la forza nucleare forte diventa man mano più debole, e i quark si comportano come se fossero quasi liberi, ovvero la costante di accoppiamento della forza nucleare forte diminuisce. Questa condizione estrema della materia, che ha caratterizzato una breve fase nell'evoluzione dell'universo primordiale, è stata riprodotta agli acceleratori di particelle come LHC del Cern, in particolare in urti ad altissima energia fra singoli nuclei di piombo, e si chiama "quark-gluon plasma". In queste condizioni in cui una grande energia è concentrata in una zona delle dimensioni di due nuclei atomici di Piombo, per un breve istante i quark e i loro collanti, che si chiamano gluoni, vagano liberi, capaci di percorrere distanze molto maggiori (anche se pur sempre infinitesime) rispetto a ciò che è loro normalmente concesso.
L'evoluzione della costante di accoppiamento della forza nucleare forte è visualizzata nel grafico qua sotto, dove sono riportate le misure effettuate a energie via via crescenti.
 |
| La costante delle interazioni forti, al contrario della costante di struttura fine, decresce con l'energia degli urti. |
Il comportamento delle interazioni nucleari forti che rende impossibile separare due quark da renderli liberi nel vuoto, si vede bene in urti osservati agli acceleratori di particelle, come quello in figura qua sotto. Nell'urto fra un elettrone e un positrone viene "creata" una coppia quark-antiquark, che si separa con grande impulso non appena prodotta. Quando il quark e l'antiquark raggiungono distanze tipiche di un decimo di miliardesimo di centimetro, (1 fm, la dimensione tipica di un protone), la forza nucleare forte, debole a distanze inferiori, diventa così intensa da impedire loro di allontanarsi ulteriormente. E' un po' come un elastico che si tende, per fare una analogia: quando i capi dell'elastico sono vicini possiamo muoverli come vogliamo, ma se cerchiamo di allontanarli troppo, l'elastico accumula energia e ci impedisce di andare oltre. A quel punto l'energia accumulata fra i due quark è così grande da "spezzare l'elastico" e materializzarsi in tante coppie di quark-antiquark formate da tutta questa energia concentrata lungo la direzione del moto dei quark iniziali. Questi quark si appiccicano immediatamente fra di loro, formando decine di particelle, che si manifestano macroscopicamente come due "jet", due spruzzate di particelle emesse in direzione opposta, orientate secondo la direzione dei due quark originari. Di eventi di questo tipo ne sono stati osservati in grande quantità, e sono la normalità negli odierni esperimenti di particelle.
 |
| Un evento a due jet di particelle, risultato della produzione di una coppia quark-antiquark con alto impulso. |
